The Galileo Energetic Particles Detector
Galileo EPD Handbook
Chapter 2. EPD Software
LGA Processing Software for the Energetic Particles Detector (continued)
Source: C. Brull and S. Stone, December 19, 1998
Appendix B. Coordinate Systems
B.1 Coordinate System Descriptions (below;
please scroll down)
B.2 Spice
B.3 Verification of Results
B.1 Coordinate System Descriptions
Position and orientation data in the Galileo LGAPROC software will be in reference to two coordinate systems: Jupiter Solar Ecliptic and Jupiter Magnetic System III. The Ephemeris Data Block contains the position of the spacecraft with respect to these two coordinate systems. The orientation data block contains the orientation of the spacecraft spin axis to these coordinate systems.
B.1.1 Jovicentric Solar Ecliptic
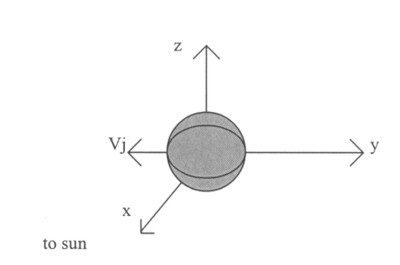
Description. Jovicentric solar ecliptic coordinates (JSE) are defined as follows. The x-axis points towards the sun. The z-axis is the cross product of Jupiter's velocity vector, V j, and the x-axis (Figure 1).
Figure 1. Jovicentric Ecliptic Coordinates
Method. The Galileo SPICE toolkit routine GSTERN_G returns a three by three transformation matrix which transforms a vector in inertial coordinates into JSE coordinates. After loading the appropriate kernels, the following FORTRAN code produces the coordinates of spacecraft location in JSE coordinates.
| C | Find the location of Galileo (object -77) in Jupiter (object 599) |
| C | centered J2000 coordinates at ephemeris time ET (ephemeris seconds past |
| C | J2000 epoch). The result is returned in the vector STARG. |
| CALLSPKEZ(-77,ET,'J2000','LT+S',599,STARG,LT) | |
| C | Get transformation matrix from J2000 to JSE coordinates at time ET. |
| C | The transformation matrix is stored in TR. |
| CALL GSETRN_G(599,ET,'J2000','LT+S',TR) | |
| C | Transform the coordinates in STARG to JSE coordinates. |
| C | JSE_STATE = TR * STARG |
| CALL MXV(TR,STARG,JSE_STATE) |
B.1.2 Jupiter Magnetic System III
Description. The Jupiter magnetic coordinate system is defined with respect to the Jovian magnetic field. Unfortunately, the magnetic axis is not simple to define. The Jovian magnetic field is far from being a simple dipole field. Models include significant quadrapole and octopole moments. The true magnetic axis is not even centered on the center of mass of Jupiter.
For the purpose of defining a coordinate system, the magnetic axis can be approximated using a centered tilted dipole, M. The Jupiter magnetic coordinate system is defined with the z-axis along the nominal dipole. The x-axis is defined as being in the system III x-z plane (Figure 2). Since this system is rotating about the an axis offset from the Jovian rotation axis, w, the longitude change for a stationary object in space will tend to speed up and slow down over the period of rotation, and the latitude of such an object will bounce up and down (1).
((1)Galileo MAGPAC Users Guide, JPL D-4714, Rev. A, June 1988.)
Figure 2. Jupiter Magnetic (System III) Coordinates

Magnetic Dipole Choices. On the basis of the Pioneer 10 and 11 measurements, two principle models(2) have emerged to represent the Jovian magnetic field in terms of spherical harmonics: the O4 model of Acuna and Ness [1976a,c] and the P 11(3,2)A model of Davis, Jones and Smith [1975]. Both contain terms up to octopole. O4 has no external terms. P 11(3,2)A also includes up to quadrapole external terms. The characteristics of the dipole terms are given in the table below:
| Model | (M) | Tilt (deg.) | λiii(1965) |
| O4 | 4.28 | 9.6 | 201.7 |
| P 11(3,2)A | 4.208 | 10 | 198.8 |
((2)Physics of the Jovian Magnetosphere, A. J. Dessler, 1983, pp. 2-5.)
System III(1965) The Jupiter system III is a left-handed Jupiter-centered system which rotates with the planet. The z-axis of the system is defined as the spin axis, ω, of Jupiter, with the positive direction oriented northward. The x-axis is fixed on the Jovian prime meridian, λIII = 0, as defined by the International Astronomical Union in 1976(3). The rotation period is defined as 9 hr 55 min 29.71 sec or 870.536 degrees/day. Longitude is measured clockwise from this prime meridian.
((3)Seidelman, P.K., and N. Devine, Evaluation of Jupiter Longitudes in System III(1965), Geophysical Research Letters, 4, 65-68, 1977.)
Method. The SPICE toolkit subroutine BODMAT returns a three by three transformation matrix from inertial J2000 coordinates to Jovicentric System III coordinates. After defining a central dipole, two rotations transform the system into magnetic coordinates. First a rotation is done about the system III y-axis to zero the x component of the dipole vector. The second rotation is about the new x-axis to zero the y component. The following FORTRAN code shows toolkit subroutines which perform the necessary operations:
| C | Find the location of Galileo (object 77) in Jupiter (object 599) |
| C | centered J2000 coordinates at ephemeris time ET (ephemeris seconds past |
| C | J2000 epoch). The result is returned in the vector STARG. |
| CALL SPKEZ(-77,ET,'J2000','LT+S',599,STARG,LT) | |
| C | Get transformation matrix from J2000 to System III coordinates at time ET. |
| C | The transformation matrix is stored in TR. |
| CALL BODMAT(599,ET,TR) | |
| C | Transform the coordinates in STARG to System III coordinates. |
| C | SysIII_STATE=TR*STARG |
| CALL MXV(TR,STARG,SYSIII_STATE) | |
| C | Now do the transformation to magnetic coordinates. |
| C | First, specify the coordinates of the magnetic axis in system III |
| C | latitude and longitude. |
| MAGLON = 158.3 * RPD ( ) ! east longitude in radians | |
| MAGLAT = 80.4 * RPD ( ) ! north latitude in radians | |
| C | Find the rotation matrix into magnetic coordinates. |
| C | Convert altitude and longitude into a x,y,z vector. |
| CALL LATREC(l.,MAGLON,MAGLAT,DIPOLE_VEC) | |
| C | Find the matrix which rotates the z-axis of the system III coordinates |
| C | to coincide with the magnetic dipole and keeps the x-axis in the |
| C | system III xz plane. |
| ANG=ACOS(DIPOLE_VEC(3)/SQRT(DIPOLE_VEC(1)**2+DIPOLE_VEC(3)**2)) | |
| IF (MPOLE(l).LT.O) THEN ANG = -ANG | |
| CALL ROTATE(ANG,2,MOUT1) | |
| CALL MXV(MOUT1,DIPOLE_VEC,DIPOLE_VEC) | |
| ANG = ATAN(DIPOLE_VEC(2)/DIPOLE_VEC(3)) | |
| CALL ROTATE(-ANG,l,MOUT2) | |
| CALL MXM(MOUT2,MOUTl,ROTATION_MATRIX) | |
| C | Transform Galileo position from system III coordinates into |
| C | magnetic coordinates |
| CALL MXV(ROTATION_MATRIX,SYSIII_STATE,MAG_STATE) |
The tilt and longitude of the dipole can be adjusted by modification of the initialization of MAGLON and MAGLAT. The resulting transformation matrix from system III to Jupiter magnetic coordinates is contained in the array ROTATION_MATRIX.
B.1.3 Magnetic Coordinates
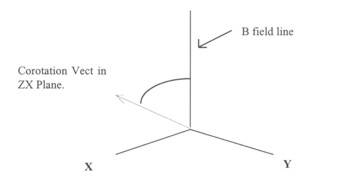
Description. Magnetic coordinates are based on the direction of the magnetic field that Galileo measures and the direction of the corotation vector. The z axis is in the direction of the magnetic field unit vector, the corotation vector lies in the xz plane, and the y axis is orthogonal to them. The process of transformation is accomplished by calculating the rotation matrix that takes the direction of the magnetic field in space craft coordinates and rotates it to point in the z direction.
Figure 3. Magnetic Coordinates
Procedure:
| C | Start with the magnetic fieldB={Bx,By,Bz} and corotation Co{Cox,Coy,Coz} in S/C coordinates. |
| C | Rotate about the y axis. angle=acos(Bz/sqrt(Bx2 + Bz2)) if Bx<0 then angle=-angle ROTVEC(B,angle,2,B1) ROTVEC(Co,angle,2,C1) ROTATE(angle,2,sc2prime) |
| C | Rotate about the new x axis. angle=-1 atan(By/Bz) ROTVEC(C1,angle,1,C1) ROTATE(angle,1,mout) MXM(mout,sc2prime,sc2prime) |
| C | Rotate about the new z axis. angle=acos(C1x/sqrt(C1x2 + C1y2)) if C1x < 0 then angle=-angle ROTATE(angle,3,mout) MXM(mout,sc2prime,sc2prime) |
| C | Apply the transformation matrix MXV(sc2prime,Co,Co) |
Next: B.2 SPICE
Return to Galileo EPD Handbook Table of Contents Page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.



