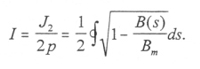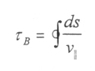Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector
Ph.D. dissertation by Shawn M. Stone, University of Kansas,
1999.
Copyright 1999 by Shawn M. Stone. Used with permission.
2.3.2 The Second Adiabatic Invariant
The invariant associated with bounce motion follows from the action integral once again:
|
|
[2.23] |
where p|| is the component of momentum along the field line and s is the distance along the field line. The vector potential term is zero since the closed particle path does not enclose any flux. From equation [2.7] and [2.22] it can be derived
|
|
[2.24] |
The second invariant is then
|
|
[2.25] |
It can be seen that the second invariant depends only on the magnetic field geometry. Equation [2.25] can rarely be integrated in closed form.
From the formalism that has been presented, it is possible to calculate the bounce period of these particles between mirror points:
|
|
[2.26] |
where using the relation for ν|| derived above gives
|
|
[2.27] |
where sm are the positions of the mirror points. This integral must normally be handled numerically, but for the dipole magnetic field model an approximate expression exists:
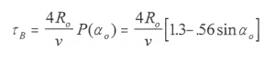 |
[2.28] |
where Ro is the radial distance out to the L shell, and αo is the equatorial pitch angle for the particles in question [Lyons and Williams, 1984; Cravens, 1997].
Next: 2.3.3 The Third Adiabatic Invariant
Return to dissertation table of contents page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.