Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector
Ph.D. dissertation by Shawn M. Stone, University of Kansas,
1999.
Copyright 1999 by Shawn M. Stone. Used with permission.
3.4 Inertial Reference Frames and Coordinate Systems
An inertial reference frame is defined as a system that is neither rotating nor accelerating relative to a certain reference point. The differential equations of motion are then represented by constant velocity terms. This provides a standard frame from which physical quantities such as position, velocity, and acceleration can be measured. The method of describing such a system in space science begins with the definition of the Z axis as the spin vector of the Earth (geographic north pole). The X axis is defined as the point where the equator of the Earth crosses the ecliptic plane of the solar system at the vernal equinox of a specific Julian date (epoch). The Y axis completes the right handed system. The stationary point that this system is referenced to is given by the star background. The current catalog of stars used is the FK4 star map, which consists of 1500 stars, and their position pins down the orientation of the inertial reference frame [U.S. Naval Observatory, 1983; Kovalevsky et al., 1989]. This geometry is shown in Figure 3.8. The Galileo spacecraft uses the position of these stars to calculate its orientation in J1950.
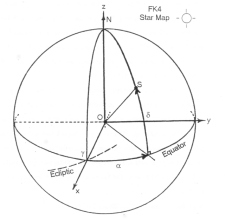 |
Figure 3.8 The inertial reference frame defined by the position of the vernal equinox γ at a certain epoch (J1950 or J2000). The X axis is defined by the point where the ecliptic plane crosses the equator at γ at the relevant epoch. The Z axis is defined by the spin axis of the Earth (North Pole). The Y axis completes the orthogonal set of the right handed inertial reference frame. For epoch J1950, 1500 stars have been cataloged from the barycenter of the solar system; this is called the FK4 catalog. A spacecraft, such as Galileo, finds its orientation from the positions of these stars [Kovalevsky et al., 1989]. |
The orientation of any object in the solar system can be calculated from the knowledge of the right ascension α and declination δ angles referenced in an equatorial system of the respective epoch. The epochs in use today are Julian date 1950 (J1950) and Julian date 2000 (J2000). For example, the orientation of the north pole of a body is specified by its right ascension αo and declination δo, while the location of the prime meridian from this point is specified by the angle W [Davies et al., 1980]. Table 3.5 shows some of these values for epoch J1950 for the Sun, Earth, and Jupiter.
Table 3.5 The standard equatorial coordinates for the north pole of the respective body in J1950. T=interval in Julian ephemeris centuries from standard epoch and d-interval in ephemeris days from the standard epoch [Davies, 1980].
| Body | Angles |
| Sun | α0=286.0° δ0=63.8° W=240.9° + 14.184° d |
| Earth | α0=0.0°- 0.640° T δ0=90.0°-0.556° T W=99.87°+360.98° d |
| Jupiter | α0=286.00°-0.008° T δ0=64.5°+.003° T WIII=80.6°+870.53° d |
3.4.1 Jovian Centered Coordinate Systems
The Jovian systems that are pertinent to this work are the Jupiter system III(1965) and Jupiter Magnetic system III coordinate systems. From the rate of modulation of the decametric radiation, the spin period of Jupiter has been calculated to be 9h 55m 29.37s [Riddle and Warwick, 1976; Berge and Gulkis, 1976]. The Jupiter system III(1965) coordinate system (Figure 3.9a) rotates with the planet at its spin rate. The z axis is the spin axis, the x axis is the system III longitude λIII(1965)=0, and y completes the orthogonal set. This system is a left-handed system with longitude increasing from East to West according to an observer at Earth. Jupiter Magnetic system III (Figure 3.9b) is based on the orientation of Jupiter's magnetic field relative to the JSIII(1965) system whose angles are based on a dipole whose magnetic axis is tilted by 9.6° relative to the JSIII(1965) Z axis and λIII(1965)= 201.7° east longitude. The Z axis is the magnetic dipole axis, the X axis lies within the plane of the JSIII XZ plane, and the Y axis completes the orthogonal set.
 |
Figure 3.9 (A) Jupiter system III(1965) coordinates. The Z axis is defined by the spin axis of Jupiter. The X axis is defined by the system III longitude λIII=0 (prime meridian). The Y axis completes the orthogonal left handed system. (B) Jupiter Magnetic system III. This system is defined by the orientation of the magnetic dipole axis in JSIII. The orientation of the dipole axis is given as θ=9.6° and λIII=201.7° [Acuna and Ness,1976]. Rotation of the dipole axis into the Z axis while maintaining the X axis of the JSMIII in the plane of the JSIII XZ plane fixes this coordinate. |
3.4.2 Ganymede Centered Coordinate Systems
The coordinate system of Ganymede can be defined in a number of ways. The longitude on Ganymede, or any other satellite for that matter, is measured from its prime meridian, which is the sub-Jovian meridian. This meridian is fixed on the Jovian satellites because the same face of each always points toward Jupiter. For Ganymede System I (Figure 3.10a), the X axis is in the direction of corotation (or orbital direction), the Y axis points toward Jupiter along the sub-Jovian meridian, and the Z axis is the spin axis of Ganymede, which can be assumed to be nearly aligned with the spin axis of Jupiter. Ganymede System II (Figure 3.10b) is rotated by 90° about the Z axis so that the X axis points toward Jupiter and the Y axis is in the anti-corotation direction.
 |
Figure 3.10 (A) Ganymede system I coordinates. The Y axis points radially towards Jupiter. The X axis points in the direction of corotation. The Z axis completes the right handed orthogonal set. (B) Ganymede system II coordinates. This system is rotated by 90° about the GSI Z axis. The X axis points toward Jupiter, the Y axis in the anti-corotation direction, and Z completes the right handed orthogonal set. |
3.4.3 Magnetic Field and Spacecraft Coordinates
The definition of magnetic field coordinates begins with the magnetic field vector at a point in the Jovian magnetosphere. The magnetic field vector is at that point defined as the Z axis. The X axis lies in the plane defined by this Z axis and the radius vector from Jupiter to the point in question. The Y axis completes the orthogonal set of this right handed coordinate system (Figure 3.11a). The pitch angles of the particles are as defined in Equation [2.6], and the phase angle is measured relative to the primed X axis according to Equation [2.7]. Spacecraft coordinates are defined relative to the spin axis of the Galileo spacecraft which is the Z axis. The Y axis is the vector normal to the step platform of the EPD instrument. The X axis completes the orthogonal set (Figure 3.11b).
 |
Figure 3.11 (A) Magnetic field coordinates. The Z axis is defined as the magnetic field vector direction. The X axis is fixed by the radius vector from Galileo to Jupiter which lies in the XZ plane. The Y axis completes the orthogonal set. (B) Spacecraft coordinates. The Z axis is the spin axis of the spacecraft. The Y axis is defined as the rotor axis for the stepping motor. The X axis completes this set. |
Next: 3.5 Coordinate Transformations and SPICE Kernels
Return to dissertation table of contents page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.



