Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector

Ph.D. dissertation by Shawn M. Stone, University of Kansas, 1999.

Copyright 1999 by Shawn M. Stone.  Used with permission.

4.1 Offset-Tilted-Dipole Models

Offset and tilted (from the source body spin axis) dipole models have typically been the first step in the representation of magnetic fields measured by spacecraft. They are desired for their simplicity and close to a body can be sufficiently accurate. For example, the Pioneer 10 data of Jupiter were initially modeled as a centered tilted dipole and an offset tilted dipole [Smith et al., 1974; Van Allen et al., 1974]. The vector magnetic field B(r) of a dipole at the origin of a body is given by

[4.1]

in MKS and coordinate free form where m is the magnetic moment of the dipole. Data along the spacecraft trajectory is fit to this model by translation of the dipole center, rotation of dipole axis, and variation of the magnetic moment strength. This process is illustrated in Figure 4.1.

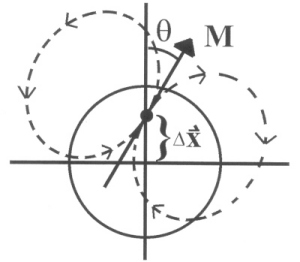Figure 4.1 Illustration of the parameters of the offset tilted dipole model in two dimensions. The center of the dipole is displaced by Δx and the dipole axis is rotated by θ from the Z axis. Generalized to three dimensions, there are 6 parameters to fit: 3 in Δx, 2 angles θ and Φ, and the magnetic moment M.

The simple OTD representation provides a convenient approximation to the field, but there are limitations to its representation of complicated field geometries. If the magnetic field is assumed to be produced by currents within a volume a, then in general, the OTD model can be expected to accurately represent the field for radial distance r >> a [Connerney, 1993]. At distances near and less than a, the field model requires consideration of higher order multipole terms.

4.2 Spherical Harmonic Models

In regions where the absence of currents is assumed, Ampere’s law, from Equation [2.1], becomes

Recognizing that the curl of a gradient is zero, B can be modeled as the gradient of a scalar potential Φ:

[4.3]

It is advantageous to expand the scalar potential in a series of spherical harmonics according to Chapman and Bartels [1940]:

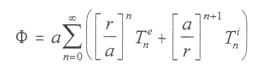[4.4]

where a is the equatorial radius of the body being modeled. The first series in increasing powers of r represents contributions due to sources external to the body, with

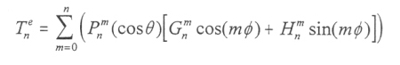[4.5]

where G_n^m and H_n^m are the external Schmidt coefficients. The second series in inverse powers of r represents the contributions due to the body’s internal sources, with

[4.6]

where g_n^m and h_n^m are the internal Schmidt coefficients. The P_n^m(cosθ) are Schmidt quasi-normalized associated Legendre functions of degree n and order m. Of course, the infinity in the summation of Equation [4.4] can be truncated at a certain n_max, which represents as many terms as is needed. The magnetic field becomes for the internal sources:

The tilt and apparent offset of the magnetic field is picked up by the m>0 terms. Table 4.1 shows the Schmidt coefficients up to n_max=3.

Table 4.1 Schmidt quasi-normalized Legendre functions to n_max=3

Next: 4.3 Modeling of External Sources: Magnetopause and Tail Fields 

Return to dissertation table of contents page.

Return to main Galileo Table of Contents Page.
Return to Fundamental Technologies Home Page.

QUICK FACTS

RELATED LINKS