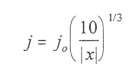Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector
Ph.D. dissertation by Shawn M. Stone, University of Kansas,
1999.
Copyright 1999 by Shawn M. Stone. Used with permission.
4.3.2 Multipole Model of the Earth's Magnetotail Field
The procedure to cast the magnetic field of the tail in terms of a multipole expansion follows the same procedure as for the magnetopause field in section 4.3.1. In a coordinate system in which the x axis is towards the sun, the z axis is anti-parallel to the Earth’s dipole, and the y axis completes the right handed system, the tail currents are all perpendicular to the x axis as shown in Figure 4.3 [Choe and Beard, 1974b]. The tail current loops start at x=-10RE and decrease in magnitude as
|
|
[4.16] |
for x<-10 Re [Behannon, 1968; Beard et al., 1970; Bird and Beard, 1972]. The current parameter, jo, is determined by the requirement that Bx of the tail field equals the measured value of 10 nT at {-60,0,5} in this Cartesian system [Choe and Beard, 1974b]. From a complex construction, the magnetic field becomes
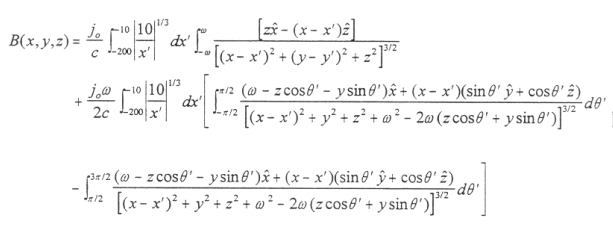 |
[4.17] |
where ω is the constant radius of the magnetocylinder taken to be 20 RE [Choe and Beard, 1974b].
The tail field is evaluated at 1256 points and then used for a least squares fitting of the first 35 terms in a spherical harmonic expansion similar to Equation [4.15]:
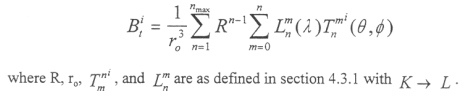 |
|
Table 4.3 shows the coefficients from the tail field for three values of the offset distance ro=10 RE up to nmax=2. Figure 4.4a shows the dipole of the Earth as given in Equation [4.8] for λ=0. This is what the field would look like if there was no other pressure impinging on it. With the addition of the magnetopause and tail currents, the familiar shape of the magnetosphere is achieved, as shown in Figure 4.4b.
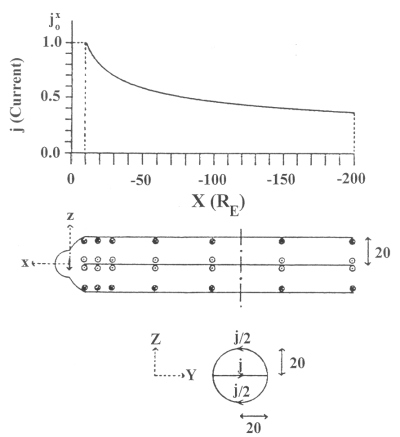 |
Figure 4.3 An illustration of the coordinates and tail current system used in the calculation of the magnetic field from the Biot-Savart law [Choe and Beard, 1974]. |
 |
Figure 4.4 (A) Dipole of the Earth with the +x axis towards the sun. (B) Dipole field of the Earth with magnetopause and tail field configuration added. |
Table 4.3 The coefficients in the series expansion of the spherical harmonics for the tail field Lnm(λ) up to nmax=2 [Choe and Beard, 1975].
| n | m | ro=10 RE |
| 1 | 0 | .02447 |
| 2 | 1 | -.01588 |
4.3.3 Magnetospheric Model of Mercury
The external multipole formalism discussed above has found use outside the magnetosphere of the Earth. When Mariner 10 made three passes past Mercury in 1973 [Hooke, 1974; Dunne 1974] a magnetic field structure was measured that was consistent with that of a magnetosphere [Ness et al., 1975]. Jackson and Beard [1977] used the model of the geomagnetic field presented above which they scaled down and re-parameterized for the difference in the physical properties of the solar wind plasma and fit to the Mercury field data to obtain a magnetospheric model for Mercury. Also included for the parameter fit was the aberration angle of magnetosphere axis relative to the solar wind plasma flow and a stand off distance of 1.4 Rm. Assuming the same magnetopause and tail configurations with the different parameters the model is fit to 295 magnetic observations [Jackson and Beard, 1977] up to nmax=7. Figures 4.5 and 4.6 show the data compared to the model along the trajectory of Mariner 10 for the first pass. Figure 4.7 shows the resulting magnetospheric shape.
 |
Figure 4.5 (A) The Bx component of the magnetic field in a system where the x axis points toward the sun and the z axis is along the rotation axis of Mercury. The data measured at Mercury is shown as a dotted line and the model is shown as a solid line. (B) The By moment of the magnetic field of Mercury [Jackson and Beard, 1977]. |
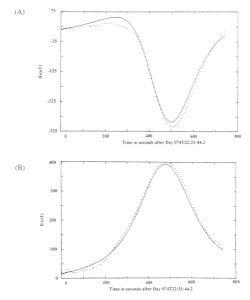 |
Figure 4.6 (A) The Bz component of the magnetic field in a system where the x axis points toward the sun and the z axis is along the rotation axis of Mercury. The data measured at Mercury is shown as a dotted line and the model is shown as a solid line. (B) The magnitude B of the magnetic field of Mercury measured along the trajectory of Mariner 10. |
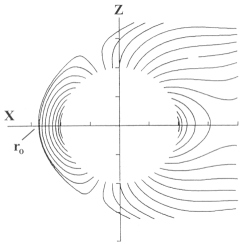 |
Figure 4.7 Meridian plane projection of the magnetosphere of Mercury as a result of the re-parameterization of the Earth multipole model with the Mercury dipole model [Jackson and Beard, 1977]. |
Next: 4.4 The O6 Multipole Model of the Jovian Internal Field
Return to dissertation table of contents page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.