Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector
Ph.D. dissertation by Shawn M. Stone, University of Kansas,
1999.
Copyright 1999 by Shawn M. Stone. Used with permission.
4.6 The Magnetodisc Current Sheet: Euler Potential Model

surfaces of constant α and β are tangential to the magnetic field at all points. The points where the surfaces of α and β intersect are the magnetic field lines [Stern, 1970].
The current sheet model discussed in section 4.4.2 is very good between 6 Rj<R<30 Rj, but doesn't recover the hinging effect of the sheet beyond 30 Rj [Connerney, 1981; Khurana, 1997]. Figure 4.13a shows an example of a current sheet fixed to the JSMIII equatorial plane. At radii beyond 30 Rj, the plasma tends to not corotate with the magnetic field of Jupiter, but is instead driven in the equatorial plane of the JSIII(1965) system [Northrop et al., 1974; Kivelson et al., 1978; Goertz, 1981], as shown in Figure 4.13b. To better represent the hinging and overall warping effect of the magnetodisk Khurana [1997] used the Euler potential formalism of Stern in a manner following Goertz [1979]. The components of the magnetic field in a cylindrical coordinate system (in JSMIII) are given by the vector components of Equation [4.23]:
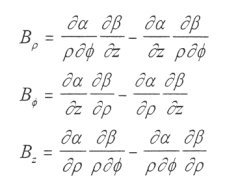 |
[4.25] |
The functional form of the Euler potentials is dictated by criteria of the hinging effect beyond 30 Rj with warping and the delay of the current sheet [Khurana, 1997]. The Euler potentials that satisfy these criteria are
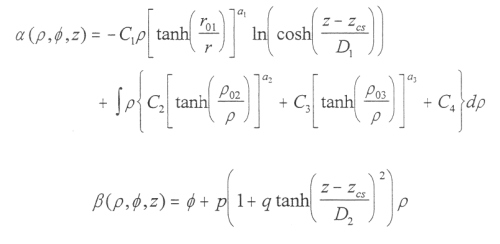 |
|
where the C, D, r01, ρ, p, and q parameters are the best fit parameters for the particular set of data being used. For the exact magnetic field components that result by putting Equations [4.26] and [4.27] into Equation [4.25], see Khurana [1997]. The best fit parameters, obtained after the removal of the O6 model, for Pioneer 10, Voyager 1, and Voyager 2 are shown in Table 4.5. Also in Table 4.5 is a column called the common model, which is a set of best fit parameters based on all three spacecraft data. Figure 4.14 shows field lines tracings from the Euler potential model compared with the vector potential model.
 |
Figure 4.13. Current sheet models [Goertz, 1976]: (A) A current sheet model that is rigidly fixed to the JSMIII plane. The Connerney model of Section 4.4.2 is an example of this type of model. (B) The current sheet geometry of a warped ring current. The hinging of the current sheet starts to affect the magnetic topology at radial distances beyond 30 Rj [Khurana, 1997]. |
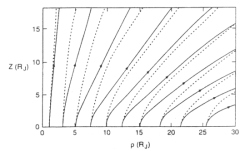 |
Figure 4.14 A comparison of the magnetic field topology of the ring current models of Khurana [1997] and Connerney [1981]. The solid lines represent the Connerney model and the dashed lines represent the Khurana model, both based on the V1 outbound pass [Khurana, 1977]. |
Table 4.5 The best fit parameters to Equations [4.25] and [4.26] for the three Jovian outbound encounters. The common model fit using data from three encounters [Khurana, 1997].
| Parameter | P10 | V1 | V2 | Common |
| C1 | 70.2 | 100.8 | 84.8 | 80.3 |
| C2 | 1369.9 | 916.4 | 1034.7 | 690.4 |
| C3 | 33.4 | 70.6 | 39.3 | 101.3 |
| C4 | -1.1 | -1.3 | -1.5 | -1.7 |
| a1 | 3.27 | 2.61 | 2.04 | 2.49 |
| a2 | 2.06 | 1.62 | 1.75 | 1.8 |
| a3 | 7.55 | 9.56 | 4.43 | 2.64 |
| r01 (Rj) | 44.1 | 35.6 | 36.7 | 38.0 |
| ρ02 | 2.55 | 1.78 | 1.99 | 2.14 |
| ρ03 | 32.8 | 27.9 | 19.7 | 12.5 |
| D1 | 1.83 | 2.16 | 2.21 | 2.01 |
| D2 | 20.60 | 19.23 | 16.81 | 13.27 |
| p | 6.66x10-3 | 7.48x10-3 | 5.73x10-3 | 6.26x10-3 |
| q | .32 | .33 | .35 | .35 |
| RMS error (nT) |
3.67 | 3.5 | 2.64 | 4.01 |
4.7 Ganymede Field: Construction of Model 1
Model 1 is comprised of the vacuum superposition of the KK96 model of the Jovian field (O6 model plus Euler potential sheet) with a tilted magnetic dipole with a surface strength of 750 nT at the equator. The north pole of the dipole is tilted by 10º from the spin axis in GSI coordinates towards 200º Ganymede east longitude [Kivelson et al., 1996, 1997]. These parameters were arrived at by the extraction of the background field from the G1 data and fit to a dipole model. Figures 1.20 to 1.23 show the field geometry of model 1 (for the G2 and G7 encounters) in GSI. From this point on, Model 1 is cast in GSII coordinates. The Jovian background field is assumed to be constant within a cubical volume with sides of 10 Rg centered on Ganymede, and is taken as uniform. The exact values used are based on vectors sampled at integer values of {x,y,z}Rg in GSII coordinates within the cubical volume from the KK96 model and are shown in Table 4.6 in GSII coordinates.
Table 4.6 Values in nT of the uniform Jovian background field used in model 1 calculated from the KK96 model [Khurana, 1997].
| Encounter/ Component |
Bx(T) | By(T) | Bz(T) |
| G2 | -.000626 | .0003 | -.000802 |
| G7 | .000723 | .00005 | -.000788 |
Next: 4.8 Ganymede Field: Construction of Model 2
Return to dissertation table of contents page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.



