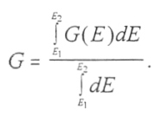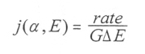Investigation of the Magnetosphere of Ganymede with Galileo's Energetic Particle Detector
Ph.D. dissertation by Shawn M. Stone, University of Kansas,
1999.
Copyright 1999 by Shawn M. Stone. Used with permission.
3.3 Count Rate and Differential Particle Flux
The particle quantity used in space science to describe trapped radiation intensities, energies, and directionality is the differential particle flux j(α, E) [Walt, 1994]. The physical quantity measured by a detector is count rate (counts/s) which must be converted to j(α, E). First, it is important to know what direction the particle was incident from (a) and what energy it possessed (E). For now, consider the generic detector in Figure 3.5 which consists of only a sensor and collimator. The detector measures particles that enter the collimator within a solid angle Ω. The finer the Ω, the finer the resolution in angular coverage. Also, as was discussed for EPD, the detector counts particles within a finite energy range or passband ΔE. The count rate for a particular channel is the integral of the differential flux over the solid angle and energy passband of the channel.
Figure 3.5 Diagram of a generic particle detector. The collimator prevents particles with trajectory α from entering the detector. Particles with trajectory β are able to enter and be counted by the sensor.

Differential flux is defined at a given location, direction, and energy as the number of particles at energy E within dE which cross a unit area dA perpendicular to the specified look direction within a unit solid angle dΩ in 1 s (see Figure 3.6a). The differential flux within an energy passband E and E+dE can then be calculated from the count rate by
|
|
[3.1] |
where A is the area of the sensor (cm2) and Ω is the collimator acceptance solid angle (steradians) in the direction of pitch angle a with respect to the magnetic field B. The quantity G = AΩ is called the geometric factor and has units of cm2 steradian. G is a measure of the sensitivity of the detector - the larger the geometric factor, the higher the counting rate of a given flux j. Of course, G only takes into consideration the actual geometry of the detector. Not all detectors are 100% efficient. The geometric factor should include a factor that takes into account the detector efficiency.
The EPD instrument uses magnetic deflection to separate and analyze charged particles. Its geometric factor varies with the energy of the particle, as illustrated in Figure 3.6b. If the geometric factor in this case is denoted G(E), then the overall geometric factor within a passband (ΔE) is
|
|
[3.2] |
The differential flux is then
|
|
[3.3] |
for each individual passband. The geometric factors of the collimator and magnetic optics system have been computer modeled by Wu and Armstrong [1988]. The results of these calculations are shown in Figure 3.7. From these curves, the energy dependent geometrical factors are calculated by integration over energy of the respective passband. The current accepted results by the EPD team for each channel are shown in Table 3.4.
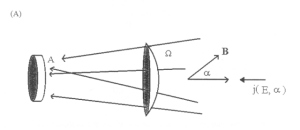  |
Figure 3.6 (A) Illustration of particle flux counted by a detector. A is the area of the detector face. All particles that enter within the solid angle Ω are counted by the detector. (B) Diagram of an energy dependent geometry factor in a passband of a detector. |
 |
Figure 3.7 Geometric factors for the LEMMS detector as calculated by Wu and Armstrong [1988]. |
Table 3.4 LEMMS geometrical factors for A, E, and F channels
| LEMMS Energy Channel | Geometrical Factor (cm2 Str) |
| A0 | 0.006 |
| A1 | 0.006 |
| A2 | 0.006 |
| A3 | 0.006 |
| A4 | 0.006 |
| A5 | 0.006 |
| A6 | 0.006 |
| A7 | 0.006 |
| E0 | 0.007 |
| E1 | 0.026 |
| E2 | 0.035 |
| E3 | 0.034 |
| F0 | 0.025 |
| F1 | 0.017 |
| F2 | 0.016 |
| F3 | 0.012 |
Next: 3.4 Inertial Reference Frames and Coordinate Systems
Return to dissertation table of contents page.
Return to main
Galileo Table of Contents Page.
Return to Fundamental
Technologies Home Page.
Updated 8/23/19, Cameron Crane
QUICK FACTS
Mission Duration: Galileo was planned to have a mission duration of around 8 years, but was kept in operation for 13 years, 11 months, and 3 days, until it was destroyed in a controlled impact with Jupiter on September 21, 2003.
Destination: Galileo's destination was Jupiter and its moons, which it orbitted for 7 years, 9 months, and 13 days.